Análisis de Relaciones
10:33 min | Última modificación: Ocutbre 13, 2021
[1]:
import warnings
warnings.filterwarnings("ignore")
[2]:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
Definición del problema
El conjunto de datos de la flor Iris contiene 150 muestras de las medidas del ancho y el largo del pétalo y del sépalo para las tres especies de esta flor (Iris setosa, Iris virginica e Iris versicolor). A partir de la muestra de datos se desean responder la siguiente pregunta:
P4.— ¿Qué relación existe entre el largo y el ancho del pétalo y el sépalo?
Carga de datos
[3]:
#
# Se cargan los datos y se realiza una inspección
# inicial de la tabla y los datos
#
iris = sns.load_dataset("iris")
display(iris.head(), iris.tail())
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 145 | 6.7 | 3.0 | 5.2 | 2.3 | virginica |
| 146 | 6.3 | 2.5 | 5.0 | 1.9 | virginica |
| 147 | 6.5 | 3.0 | 5.2 | 2.0 | virginica |
| 148 | 6.2 | 3.4 | 5.4 | 2.3 | virginica |
| 149 | 5.9 | 3.0 | 5.1 | 1.8 | virginica |
Análisis
[4]:
iris_melt = pd.melt(
iris,
id_vars="species",
var_name="Variables",
value_name="Values",
)
[5]:
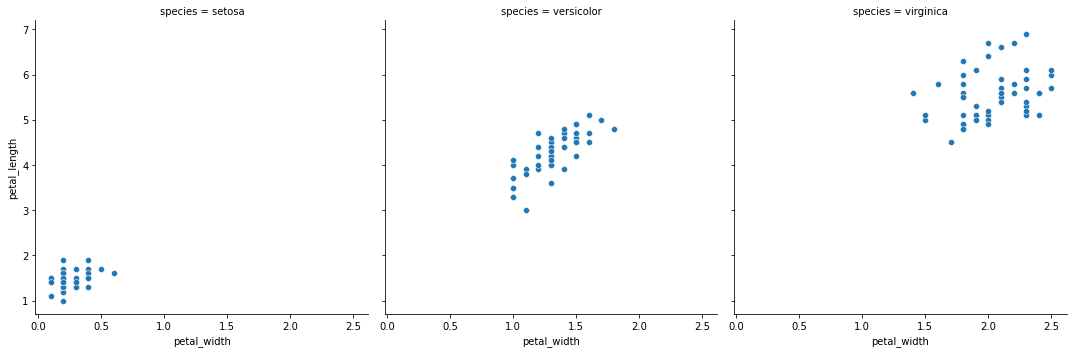
sns.relplot(
x="petal_width",
y="petal_length",
col="species",
data=iris,
)
plt.show()
[6]:
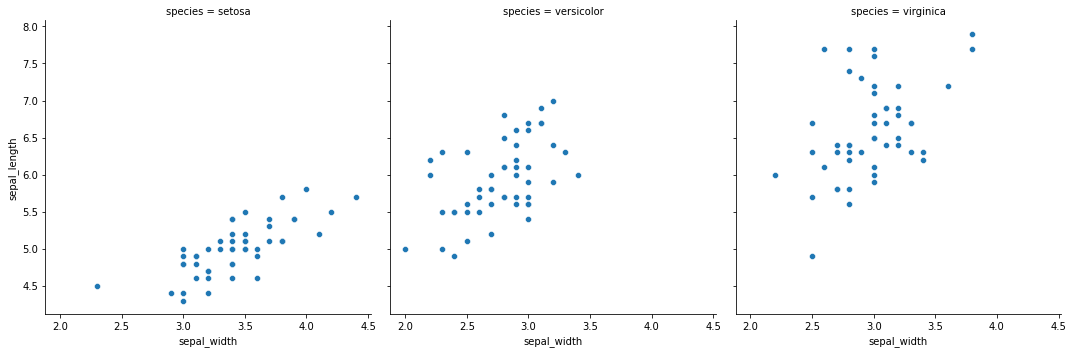
sns.relplot(
x="sepal_width",
y="sepal_length",
col="species",
data=iris,
)
plt.show()
[7]:
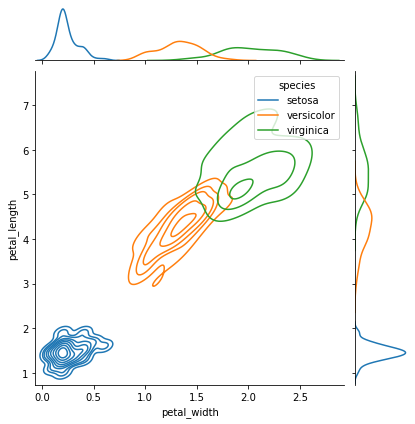
sns.jointplot(
data=iris,
x="petal_width",
y="petal_length",
hue="species",
kind="kde",
)
plt.show()
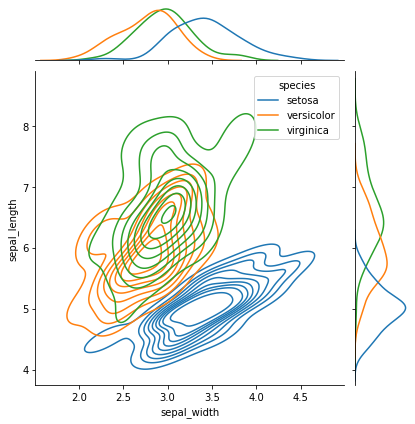
[8]:
sns.jointplot(
data=iris,
x="sepal_width",
y="sepal_length",
hue="species",
kind="kde",
)
plt.show()
Covarianza
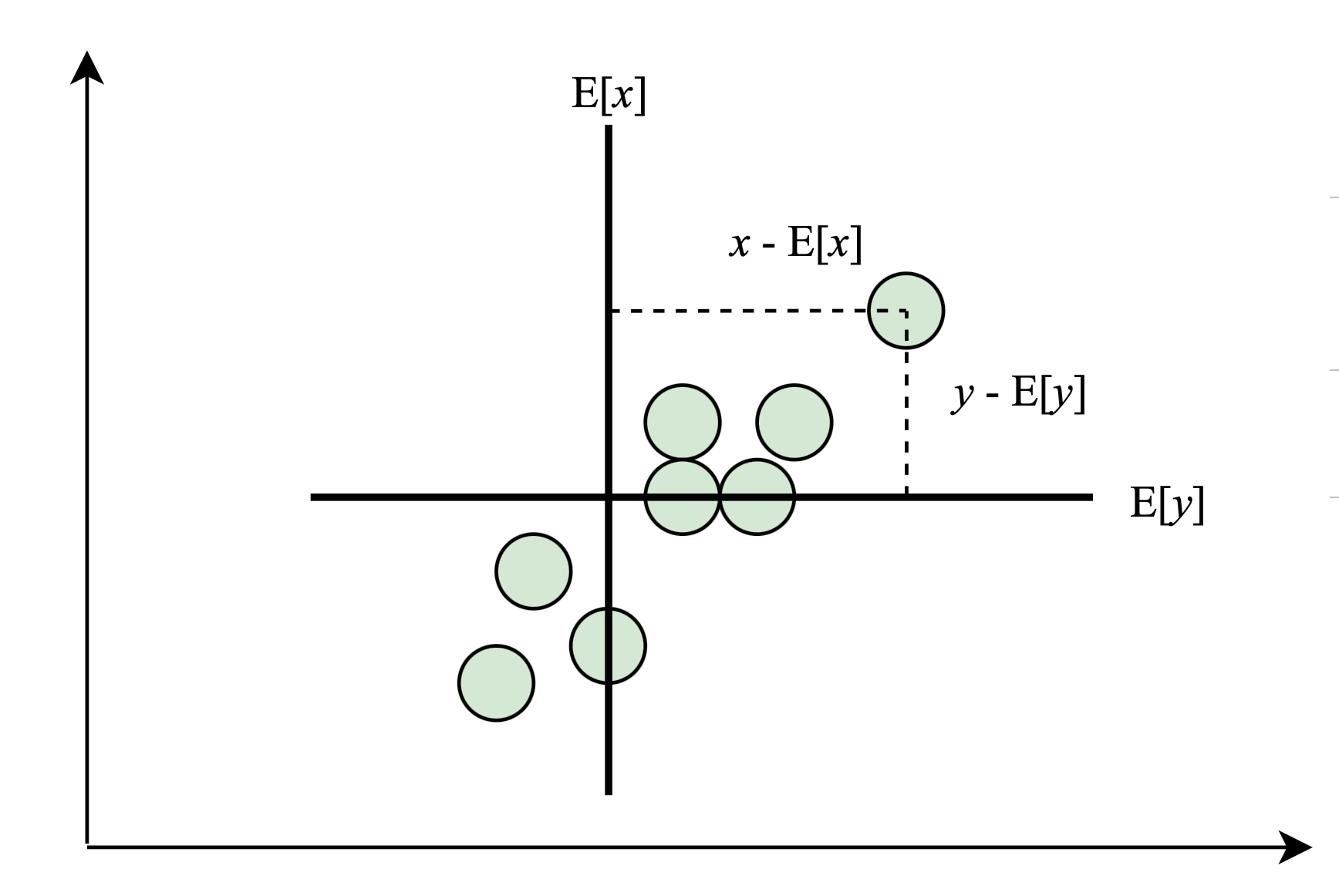
[9]:
np.cov(iris.petal_length, iris.sepal_length)
[9]:
array([[3.11627785, 1.27431544],
[1.27431544, 0.68569351]])
[10]:
iris.cov()
[10]:
| sepal_length | sepal_width | petal_length | petal_width | |
|---|---|---|---|---|
| sepal_length | 0.685694 | -0.042434 | 1.274315 | 0.516271 |
| sepal_width | -0.042434 | 0.189979 | -0.329656 | -0.121639 |
| petal_length | 1.274315 | -0.329656 | 3.116278 | 1.295609 |
| petal_width | 0.516271 | -0.121639 | 1.295609 | 0.581006 |
Coeficiente de correlación
Métrica que representa la dependencia entre una variable y otra. El coeficiente de correlación de Pearson \(r\) entre dos variables \(x\) y \(y\) se calcula como:
La correlación va entre \(-1\) (correlación perfecta negativa) y \(+1\) (correlación perfecta positiva). Un valor de \(0\) indica que no hay correlación.
[11]:
np.corrcoef(iris.sepal_length, iris.petal_length)
[11]:
array([[1. , 0.87175378],
[0.87175378, 1. ]])
Matriz de correlación
Matriz donde cada fila y cada columna corresponde a una variable, y los elementos corresponden a la correlación entre las respectivas variables.
[12]:
iris.corr()
[12]:
| sepal_length | sepal_width | petal_length | petal_width | |
|---|---|---|---|---|
| sepal_length | 1.000000 | -0.117570 | 0.871754 | 0.817941 |
| sepal_width | -0.117570 | 1.000000 | -0.428440 | -0.366126 |
| petal_length | 0.871754 | -0.428440 | 1.000000 | 0.962865 |
| petal_width | 0.817941 | -0.366126 | 0.962865 | 1.000000 |
[13]:
sns.heatmap(
iris.corr(),
xticklabels=iris.columns.values,
yticklabels=iris.columns.values,
)
plt.show()
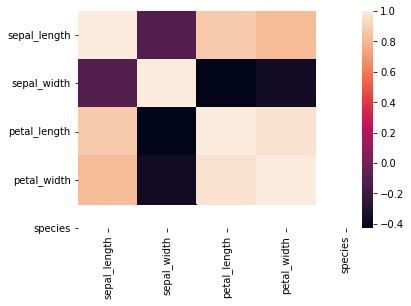
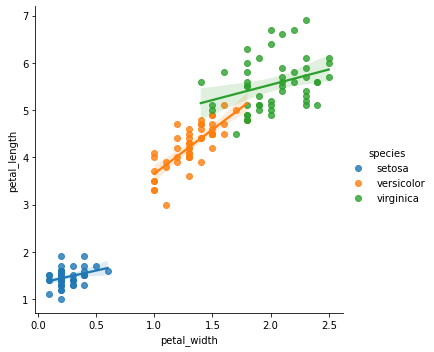
Regresión
[14]:
sns.lmplot(
x="petal_width",
y="petal_length",
data=iris,
hue="species",
)
plt.show()
[15]:
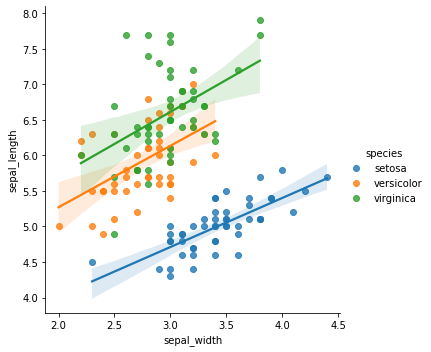
sns.lmplot(
x="sepal_width",
y="sepal_length",
data=iris,
hue="species",
)
plt.show()