Medidas de Dispersión

• 18:39 min | Última modificación: Dicimebre 13, 2021 | YouTube

import warnings

warnings.filterwarnings("ignore")

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns

Definición del problema

El conjunto de datos de la flor Iris contiene 150 muestras de las medidas del ancho y el largo del pétalo y del sépalo para las tres especies de esta flor (Iris setosa, Iris virginica e Iris versicolor). A partir de la muestra de datos se desean responder la siguiente pregunta:

• P2.— ¿Cuál es el rango típico de la longitud y ancho del pétalo y del sépalo para cada uno de los tipos de flores?

Carga de datos

#
# Se cargan los datos y se realiza una inspección
# inicial de la tabla y los datos
#
iris = sns.load_dataset('iris')

display(
    iris.head(),
    iris.tail()
)

	sepal_length	sepal_width	petal_length	petal_width	species
0	5.1	3.5	1.4	0.2	setosa
1	4.9	3.0	1.4	0.2	setosa
2	4.7	3.2	1.3	0.2	setosa
3	4.6	3.1	1.5	0.2	setosa
4	5.0	3.6	1.4	0.2	setosa

	sepal_length	sepal_width	petal_length	petal_width	species
145	6.7	3.0	5.2	2.3	virginica
146	6.3	2.5	5.0	1.9	virginica
147	6.5	3.0	5.2	2.0	virginica
148	6.2	3.4	5.4	2.3	virginica
149	5.9	3.0	5.1	1.8	virginica

P2.— ¿Cuál es el rango típico de la longitud y ancho del pétalo y del sépalo para cada uno de los tipos de flores?

Esta pregunta se refiere a una medida de la dispersión o variabilildad de los datos y a como se distribuyen.

Métricas basadas en la distancia respecto a las métricas de localización

Desviación:

Diferencia entre el valor observado y el valor estimado de localización. En modelado sus sinónimos son errores o residuales.

Rango:

Diferencia entre el valor más grande y más pequeño de la muestra de los datos.

iris_melt = pd.melt(
    iris,
    id_vars="species",
    var_name="Variables",
    value_name="Values",
)

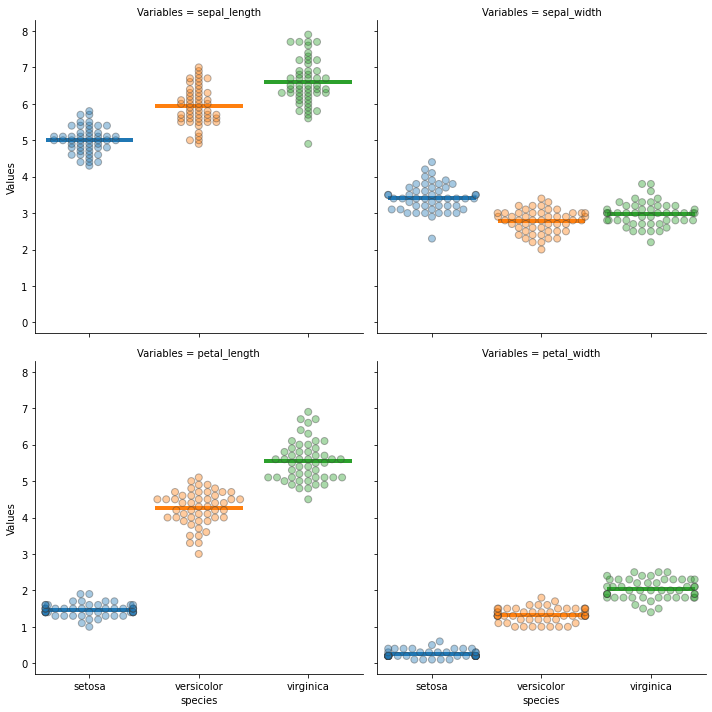
g = sns.catplot(
    x="species",
    y="Values",
    data=iris_melt,
    col="Variables",
    kind="swarm",
    col_wrap=2,
    alpha=0.4,
    s=7,
    edgecolors="k",
    linewidth=1,
)

colors = ['tab:blue', 'tab:orange', 'tab:green']

means = iris.groupby("species").mean()

for i_axes in range(4):
    ax = g.axes[i_axes]
    x_lim = ax.get_xlim()
    mean_values = means[means.columns[i_axes]]
    for i, (color, mean_value) in enumerate(zip(colors, mean_values)):
        g.axes[i_axes].hlines(mean_value, i-0.4, i+0.4,  ls='-', color=color, lw=4)

plt.show()

Varianza muestral:

\[s^2 = \frac{1}{n-1} \sum_{i=1}^n (x_i - \bar{x})^2\]

#
# Cálculo para una variable
#
from statistics import variance

display(
    iris.sepal_length.var(),
    variance(iris.sepal_length),
    np.var(iris.sepal_length),
)

0.6856935123042507

0.6856935123042506

0.6811222222222223

#
# Cálculo para las columnas del dataframe
#
iris.var()

sepal_length    0.685694
sepal_width     0.189979
petal_length    3.116278
petal_width     0.581006
dtype: float64

#
# Cálculo por especie
#
iris.groupby('species').var()

	sepal_length	sepal_width	petal_length	petal_width
species
setosa	0.124249	0.143690	0.030159	0.011106
versicolor	0.266433	0.098469	0.220816	0.039106
virginica	0.404343	0.104004	0.304588	0.075433

Desviación estándar muestral.

Raíz cuadrada de la varianza muestral.

#
# Cálculo para una variable
#
from statistics import stdev

display(
    iris.sepal_length.std(),
    stdev(iris.sepal_length),
    np.std(iris.sepal_length),
)

0.828066127977863

0.8280661279778629

0.8253012917851409

#
# Cálculo para las columnas del dataframe
#
iris.std()

sepal_length    0.828066
sepal_width     0.435866
petal_length    1.765298
petal_width     0.762238
dtype: float64

#
# Cálculo por especie
#
iris.groupby('species').std()

	sepal_length	sepal_width	petal_length	petal_width
species
setosa	0.352490	0.379064	0.173664	0.105386
versicolor	0.516171	0.313798	0.469911	0.197753
virginica	0.635880	0.322497	0.551895	0.274650

Desviación media absoluta (MAD):

Norma L1 o distancia de Manhattan.

\[\text{MAD} = \frac{1}{n} \sum_{i=1}^n |x_i - \bar{x}|\]

#
# Cálculo para una variable
#
from scipy.stats import median_absolute_deviation

display(
    iris.sepal_length.mad(),
    median_absolute_deviation(iris.sepal_length)
)

0.6875555555555557

1.0378200000000002

#
# Cálculo para las columnas del dataframe
#
iris.mad()

sepal_length    0.687556
sepal_width     0.336782
petal_length    1.562747
petal_width     0.658133
dtype: float64

#
# Cálculo por especie
#
iris.groupby('species').mad()

	sepal_length	sepal_width	petal_length	petal_width
species
setosa	0.27072	0.28736	0.13152	0.08256
versicolor	0.42144	0.25480	0.37920	0.15712
virginica	0.50256	0.24216	0.44000	0.22808

Desviación absoluta de la mediana:

Ya que la varianza y la desviación media absoluta no son robusta a outliers, se puede realizar un estimado de la desviación usando la mediana \(m\) de la muestra:

\[\text{Mediana}(|x_1 - m|,\; |x_2 - m|,\;...,\;|x_n - m|)\]

También es posible computar la varianza muestral truncada en analogía a la media truncada.

def madm(df):
    d = df._get_numeric_data().copy()
    m = d.median()
    for c in d.columns:
        d[c] = d[c] - m[c]
    return d.mad()


madm(iris)

sepal_length    0.687556
sepal_width     0.336782
petal_length    1.562747
petal_width     0.658133
dtype: float64

#
# Cálculo por especie
#
def madm(x):
    m = x.median()
    x = x - m
    x = x.abs()
    return x.mean()


iris.groupby('species').agg(madm)

	sepal_length	sepal_width	petal_length	petal_width
species
setosa	0.270	0.284	0.130	0.066
versicolor	0.420	0.250	0.376	0.154
virginica	0.492	0.238	0.440	0.226

Métricas basadas en la distribución de los datos

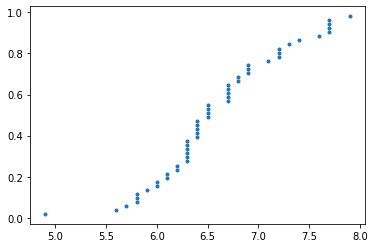
Función de Densidad Acumulada Empírica (ECDF)

def ecdf(ax, data, param_dict=None):

    if param_dict is None:
        param_dict = {}

    props = {
        'marker': '.',
        'linestyle': 'none',
    }

    props = {**props, **param_dict}

    x = np.sort(data)
    y = np.arange(1, len(data) + 1) / (len(data) + 1)
    out = ax.plot(x, y, **props)
    return out


_, ax = plt.subplots(1, 1)
ecdf(ax, iris.sepal_length[iris.species == 'virginica'])
plt.show()

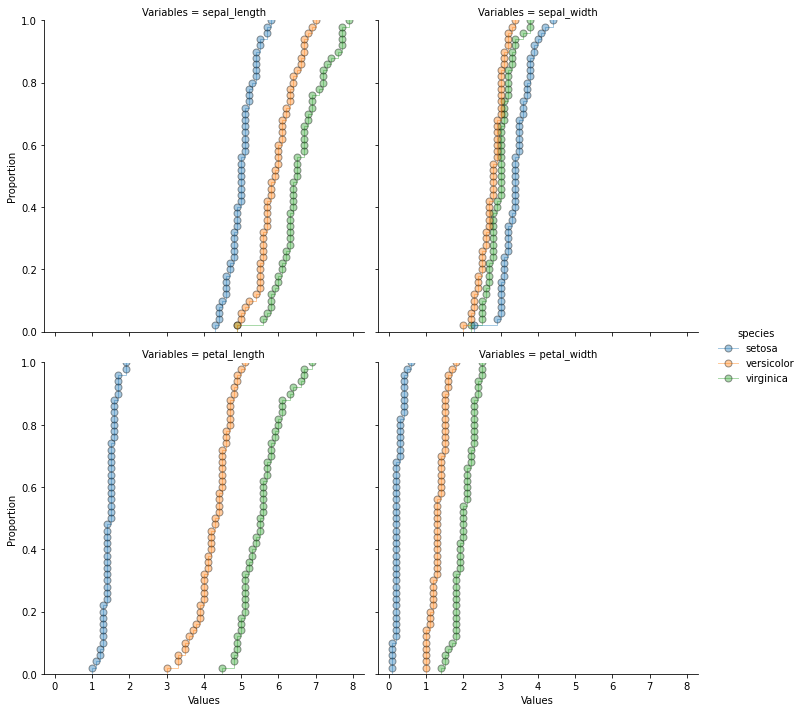
sns.displot(
    kind="ecdf",
    x="Values",
    hue='species',
    data=iris_melt,
    col="Variables",
    col_wrap=2,
    marker='o',
    linestyle=None,
    alpha=0.4,
    markersize=7,
    markeredgecolor="k",
    linewidth=1,
)
plt.show()

Estadísticos de orden: Métricas calculadas sobre los datos ordenados.

• Percentil \(p\): Valor para el cual el \(p\) por ciento de los datos son menores o iguales.

• decil \(d\): Valor para el cual el \(d\) por ciento de los datos son menores o iguales. \(d\) es un múltiplo de 10.

• Cuartil inferior: Valor para el cual el 25% de las observaciones son más pequeñas (percentil del 25%).

• Cuartil superior: Valor para el cual el 25% de las observaciones son más grandes (percentil del 75%).

• Rango intercuartil (IQR):

\[\text{IQR} = \text{Cuartil superior} - \text{Cuartil inferior}\]

#
# Cálculo de los cuartiles
#
iris.quantile(
    # -------------------------------------------------------------------------
    # the quantile(s) to compute
    q=[0.25, 0.75],
    # -------------------------------------------------------------------------
    # Specifies the interpolation method to use, when the desired quantile lies
    # between two data points i and j:
    # {‘linear’, ‘lower’, ‘higher’, ‘midpoint’, ‘nearest’}
    interpolation='linear',
)

	sepal_length	sepal_width	petal_length	petal_width
0.25	5.1	2.8	1.6	0.3
0.75	6.4	3.3	5.1	1.8

#
# Cálculo de cuartiles
#
display(
    iris.quantile(0.25),
    iris.quantile(0.75)
)

sepal_length    5.1
sepal_width     2.8
petal_length    1.6
petal_width     0.3
Name: 0.25, dtype: float64

sepal_length    6.4
sepal_width     3.3
petal_length    5.1
petal_width     1.8
Name: 0.75, dtype: float64

iris.groupby("species").quantile(0.25)

	sepal_length	sepal_width	petal_length	petal_width
species
setosa	4.800	3.200	1.4	0.2
versicolor	5.600	2.525	4.0	1.2
virginica	6.225	2.800	5.1	1.8

iris.groupby("species").quantile(0.75)

	sepal_length	sepal_width	petal_length	petal_width
species
setosa	5.2	3.675	1.575	0.3
versicolor	6.3	3.000	4.600	1.5
virginica	6.9	3.175	5.875	2.3

iris.groupby("species").quantile(0.75) - iris.groupby("species").quantile(0.25)

	sepal_length	sepal_width	petal_length	petal_width
species
setosa	0.400	0.475	0.175	0.1
versicolor	0.700	0.475	0.600	0.3
virginica	0.675	0.375	0.775	0.5

#
# El método describe de pandas computa los principales estadísticos para las
# columnas numéricas del dataframe
#
iris.describe()

	sepal_length	sepal_width	petal_length	petal_width
count	150.000000	150.000000	150.000000	150.000000
mean	5.843333	3.057333	3.758000	1.199333
std	0.828066	0.435866	1.765298	0.762238
min	4.300000	2.000000	1.000000	0.100000
25%	5.100000	2.800000	1.600000	0.300000
50%	5.800000	3.000000	4.350000	1.300000
75%	6.400000	3.300000	5.100000	1.800000
max	7.900000	4.400000	6.900000	2.500000

for column in iris._get_numeric_data().columns:
    print(column)
    print(iris.groupby("species")[column].describe())
    print("")

sepal_length
            count   mean       std  min    25%  50%  75%  max
species
setosa       50.0  5.006  0.352490  4.3  4.800  5.0  5.2  5.8
versicolor   50.0  5.936  0.516171  4.9  5.600  5.9  6.3  7.0
virginica    50.0  6.588  0.635880  4.9  6.225  6.5  6.9  7.9

sepal_width
            count   mean       std  min    25%  50%    75%  max
species
setosa       50.0  3.428  0.379064  2.3  3.200  3.4  3.675  4.4
versicolor   50.0  2.770  0.313798  2.0  2.525  2.8  3.000  3.4
virginica    50.0  2.974  0.322497  2.2  2.800  3.0  3.175  3.8

petal_length
            count   mean       std  min  25%   50%    75%  max
species
setosa       50.0  1.462  0.173664  1.0  1.4  1.50  1.575  1.9
versicolor   50.0  4.260  0.469911  3.0  4.0  4.35  4.600  5.1
virginica    50.0  5.552  0.551895  4.5  5.1  5.55  5.875  6.9

petal_width
            count   mean       std  min  25%  50%  75%  max
species
setosa       50.0  0.246  0.105386  0.1  0.2  0.2  0.3  0.6
versicolor   50.0  1.326  0.197753  1.0  1.2  1.3  1.5  1.8
virginica    50.0  2.026  0.274650  1.4  1.8  2.0  2.3  2.5

#
# Método describe aplicado a una columna particular
#
iris.sepal_length.describe()

count    150.000000
mean       5.843333
std        0.828066
min        4.300000
25%        5.100000
50%        5.800000
75%        6.400000
max        7.900000
Name: sepal_length, dtype: float64

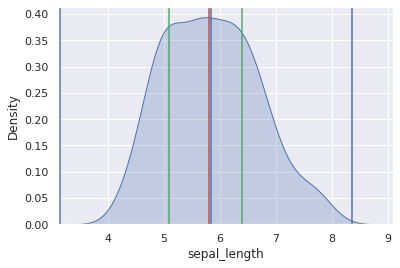
descriptive_stats = iris.sepal_length.describe()

q75 = iris.sepal_length.describe()['75%']
q25 = iris.sepal_length.describe()['25%']
iqr = q75 - q25

upper_outliers = q75 + 1.5 * iqr
lower_outliers = q25 - 1.5 * iqr

sns.set(color_codes=True)

sns.kdeplot(iris['sepal_length'], shade=True)
plt.axvline(iris.sepal_length.mean())
plt.axvline(iris.sepal_length.median(), color='r')
plt.axvline(q25, color='g')
plt.axvline(q75, color='g')
plt.axvline(upper_outliers, color = 'b')
plt.axvline(lower_outliers, color = 'b')
plt.show()

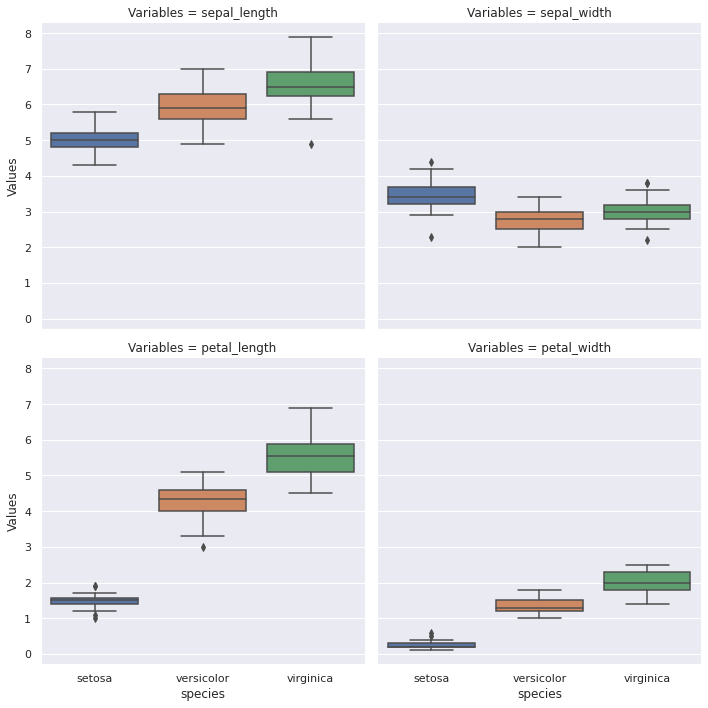
Diagramas de caja y bigote

#
# La caja central representa los cuartiles del 25% y 75%.
# La línea centra de la caja representa la mediana
# Los bigotes están ubicados a 1.5 veces el rango interquartil.
# Los puntos por fuera de los bigotes representan outliers.
#
sns.catplot(
    x="species",
    y="Values",
    data=iris_melt,
    col="Variables",
    kind="box",
    col_wrap=2,
)
plt.show()

Medidas de forma

from scipy.stats import skew

display(
    iris.sepal_length.skew(),
    skew(iris.sepal_length),
)

0.3149109566369728

0.3117530585022963

from scipy.stats import kurtosis

display(
    iris.sepal_length.kurt(),
    kurtosis(iris.sepal_length),
)

-0.5520640413156395

-0.5735679489249765