Medidas de Localización
17:13 min | Última modificación: Ocutbre 15, 2021 | YouTube
[1]:
import warnings
warnings.filterwarnings("ignore")
[2]:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
Definición del problema
El conjunto de datos de la flor Iris contiene 150 muestras de las medidas del ancho y el largo del pétalo y del sépalo para las tres especies de esta flor (Iris setosa, Iris virginica e Iris versicolor). A partir de la muestra de datos se desean responder la siguiente pregunta:
P1.— ¿Cuál es la longitud y ancho típicos del pétalo y del sépalo para cada uno de los tis de flores?
Carga de datos
[3]:
#
# Se cargan los datos y se realiza una inspección
# inicial de la tabla y los datos
#
iris_df = sns.load_dataset("iris")
display(iris_df.head(), iris_df.tail())
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 145 | 6.7 | 3.0 | 5.2 | 2.3 | virginica |
| 146 | 6.3 | 2.5 | 5.0 | 1.9 | virginica |
| 147 | 6.5 | 3.0 | 5.2 | 2.0 | virginica |
| 148 | 6.2 | 3.4 | 5.4 | 2.3 | virginica |
| 149 | 5.9 | 3.0 | 5.1 | 1.8 | virginica |
P1.— ¿Cuál es la longitud y ancho típicos del pétalo y del sépalo para cada uno de los tipos de flores?
En esta pregunta se esta pidiendo una medida o estimación de localización del valor típico de la longitud del pétalo. Existen varias medidas.
[4]:
iris_melt = iris_df.copy()
iris_melt = pd.melt(
iris_melt,
id_vars="species",
var_name="Variables",
value_name="Values",
)
iris_melt.head()
[4]:
| species | Variables | Values | |
|---|---|---|---|
| 0 | setosa | sepal_length | 5.1 |
| 1 | setosa | sepal_length | 4.9 |
| 2 | setosa | sepal_length | 4.7 |
| 3 | setosa | sepal_length | 4.6 |
| 4 | setosa | sepal_length | 5.0 |
[5]:
#
# Esta gráfica permite comparar los valores de las variables para una misma
# especie (no muy util para inferir conclusiones)
#
sns.catplot(
x="Variables",
y="Values",
data=iris_melt,
col="species",
kind="swarm",
)
plt.show()

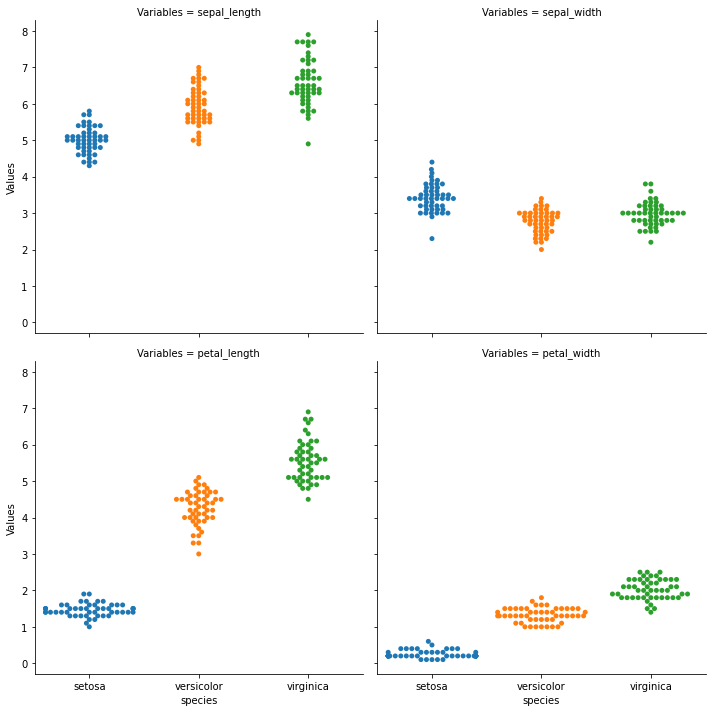
[6]:
#
# Esta gráfica permite comparar una variable entre especies
#
sns.catplot(
x="species",
y="Values",
data=iris_melt,
col="Variables",
kind="swarm",
col_wrap=2,
)
plt.show()
Media o promedio muestral:
Valor “típico” de los datos.
[7]:
#
# Cálculo para una variable
#
from statistics import mean
display(
iris_df.sepal_length.mean(),
mean(iris_df.sepal_length),
np.mean(iris_df.sepal_length),
)
5.843333333333334
5.843333333333334
5.843333333333334
[8]:
#
# Cálculo para las columnas numéricas del
# dataframe
#
iris_df.mean()
[8]:
sepal_length 5.843333
sepal_width 3.057333
petal_length 3.758000
petal_width 1.199333
dtype: float64
[9]:
#
# Cálculo de la media de cada columna por especie
#
iris_df.groupby("species").mean()
[9]:
| sepal_length | sepal_width | petal_length | petal_width | |
|---|---|---|---|---|
| species | ||||
| setosa | 5.006 | 3.428 | 1.462 | 0.246 |
| versicolor | 5.936 | 2.770 | 4.260 | 1.326 |
| virginica | 6.588 | 2.974 | 5.552 | 2.026 |
Media ponderada:
Outlier o valor atípico:
Valores extremadamente distantes del resto de los datos. En algunos casos se pueden definir en términos de la media y la desviación estándar de la muestra; por ejemplo, se considera outliers aquellas observaciones distantes más de 3.5\(\sigma\) de la media.
Media truncada:
Se calcula la media sobre los datos después de eliminar los \(p\) datos más pequeños y los \(p\) datos más grandes. Si \(x_{(1)}\), \(x_{2}\), …, \(x_{(n)}\) representan los datos ordenados, donde \(x_{(1)}\) es el dato más pequeño y \(x_{(n)}\) el más grande, entonces la media truncada se calcula como:
Mediana:
Es el valor \(x_{((n+1)/2)}\) cuando se ordenan los datos. Es una aproximación robusta (no influenciada por datos atípicos o distribuciones asimétricas.
[10]:
#
# Cálculo para una variable
#
from statistics import median
display(
iris_df.sepal_length.median(),
median(iris_df.sepal_length),
np.median(iris_df.sepal_length),
)
5.8
5.8
5.8
[11]:
#
# Cálculo para las columnas del dataframe
#
iris_df.median()
[11]:
sepal_length 5.80
sepal_width 3.00
petal_length 4.35
petal_width 1.30
dtype: float64
[12]:
#
# Cálculo discriminando por especie
#
iris_df.groupby("species").median()
[12]:
| sepal_length | sepal_width | petal_length | petal_width | |
|---|---|---|---|---|
| species | ||||
| setosa | 5.0 | 3.4 | 1.50 | 0.2 |
| versicolor | 5.9 | 2.8 | 4.35 | 1.3 |
| virginica | 6.5 | 3.0 | 5.55 | 2.0 |
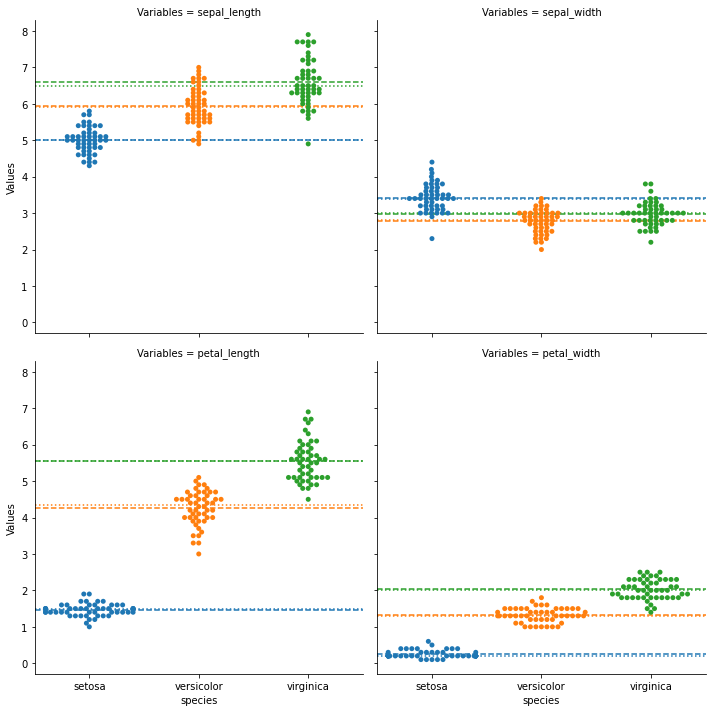
[13]:
g = sns.catplot(
x="species",
y="Values",
data=iris_melt,
col="Variables",
kind="swarm",
col_wrap=2,
)
colors = ['tab:blue', 'tab:orange', 'tab:green']
means = iris_df.groupby("species").mean()
medians = iris_df.groupby("species").median()
for i_axes in range(4):
ax = g.axes[i_axes]
mean_values = means[means.columns[i_axes]]
median_values = medians[medians.columns[i_axes]]
for color, mean_value, median_value in zip(colors, mean_values, median_values):
g.axes[i_axes].axhline(mean_value, ls='--', color=color)
g.axes[i_axes].axhline(median_value, ls=':', color=color)
plt.show()
Moda:
[14]:
#
# Cálculo para una variable
#
from statistics import mode
from scipy import stats
display(
iris_df.sepal_length.mode(),
mode(iris_df.sepal_length),
stats.mode(iris_df.sepal_length),
)
0 5.0
dtype: float64
5.0
ModeResult(mode=array([5.]), count=array([10]))
[15]:
#
# Cálculo para las columnas del dataframe
#
iris_df.mode()
[15]:
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.0 | 3.0 | 1.4 | 0.2 | setosa |
| 1 | NaN | NaN | 1.5 | NaN | versicolor |
| 2 | NaN | NaN | NaN | NaN | virginica |